Rovnice s neznámou ve jmenovateli 2

$\frac{2x+19}{5x^{2}-5}-3=\frac{17}{x^{2}-1}+\frac{3x}{1-x}\;/\times 5(x^{2}-1)$

$2x+19-15(x^{2}-1)=85-15x(x+1)$

$2x+19-15x^{2}-15=85-15x^{2}-15$

$17x=51$

$x=3$

$x\neq +1$

$x\neq -1$

$K=\left \{3 \right \}$

$\frac{x}{2(x-2)}-1=\frac{10x-8}{3(2-x}+\frac{1+2x}{x-2}$

$\frac{x}{2(x-2)}-1=\frac{10x-8}{-3(x-2}+\frac{1+2x}{x-2}\;/\times -6(x-2)$

$-3x+6(x-2)=2(10x-8)-6(1+2x)$

$-3x+6x-12=20x-16-6-12x$

$3x-12=8x-22$

$-5x=-10$

$x=2$

$x\neq 2$

$K=\left \{ \;\;\; \right \}$

$2-\frac{6}{2x-6}=\frac{2x+1}{3-x}$

$2-\frac{6}{2(x-3)}=\frac{2x+1}{-(x-3)}\;/\times -2(x-3)$

$-4(x-3)+6=2(2x+1)$

$-4x+18=4x+2$

$-8x=-16$

$x=2$

$x\neq 3$

$K=\left \{2 \right \}$

$\frac{7x+2}{3x-2}-\frac{9}{2(2-3x)}=\frac{10x-4}{3(3x-2)}-\frac{1}{16}$

$\frac{7x+2}{3x-2}+\frac{9}{2(3x-2)}=\frac{10x-4}{3(3x-2)}-\frac{1}{16}\;/\times 48(3x-2)$

$48(7x+2)+24\times 9=16(10x-4)-3(3x-2)$

$336x+96+216=160x-64-9x+6$

$336x+312=151x-58$

$185x=-370$

$x=-2$

$x\neq \frac{2}{3}$

$K=\left \{-2 \right \}$

$\frac{x+2}{x-2}-1=\frac{3x^{2}+x+9}{3(x^{2}-4}-\frac{x-2}{x+2}\;/\times 3(x^{2}-4)$

$3(x+2)^{2}-3(x^{2}-4)=3x^{2}+x+9-3(x-2)^{2}$

$3(x^{2}+4x+4)-3x^{2}+12=3x^{2}+x+9-3(x^{2}-4x+4)$

$3x^{2}+12x+12-3x^{2}+12=3x^{2}+x+9-3x^{2}+12x-12$

$12x+24=13x-3$

$-x=-27$

$x=27$

$x\neq +2$

$x\neq -2$

$K=\left \{27 \right\}$

$\frac{2x+4}{x-6}-1<0$

$\frac{2x+4-x+6}{x-6}<0$

$\frac{x+10}{x-6}<0$

$nulové\;body=-10;6$

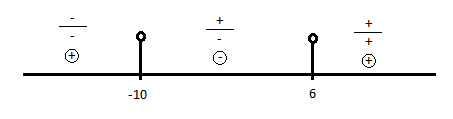
$K=(-10;6)$

Postup: 

1. Zakreslíme nulové body na osu.

2. Zvolíme libovolné číslo z každého intervalu a zjistíme, jaké znaménko bude mít výraz ve zlomku.

3. Do kroužku si zapíšeme výsledné znaménko zlomku.

4. Podle výsledného znaménko vybereme interval odpovídající zadání.

5. Musíme také rozhodnout, zda zadání vyhovují nulové body, tzn. zda patří nebo nepatří do výsledného intervalu. Do intervalu nikdy nepatří nulový bod, který jsme získali ze jmenovatele zlomku. Pokud je v nerovnici znaménko větší nebo menší, tak ani nulový bod z čitatele zlomku nezahrneme do výsledného intervalu (prázné kolečko a kulatá závorka). Pokud je znaménko menší nebo rovno nebo větší nebo rovno, tak nulový bod z čitatele do intervalu patří (plné kolečko a ostrá závorka).

$\frac{1}{x-1}-2\leq 0$

$\frac{1-2x+2}{x-1}\leq 0$

$\frac{-2x+3}{x-1}\leq 0$

$nulové\;body=1;\frac{3}{2}$

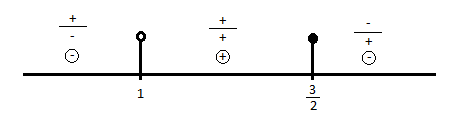
$K= (-\infty;1) \cup \left \langle \frac{3}{2};\infty \right )$

$\frac{3x-1}{5+2x}>0$

$nulové\;body=-\frac{5}{2};\frac{1}{3}$

$K= (-\infty;-\frac{5}{2}) \cup \left \langle \frac{1}{3};\infty \right )$

$nulové\;body=\frac{3}{2};\frac{7}{3}$

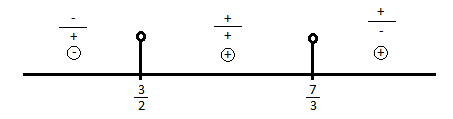
$K=(\frac{3}{2};\frac{7}{3})$

$nulové\;body=-\frac{8}{5};\frac{7}{3}$

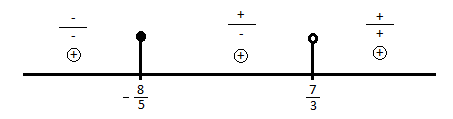
$K= (-\infty;-\frac{8}{5}) \cup \left \langle \frac{7}{3};\infty \right )$