Příprava na přijímací zkoušky SŠ
TEST č. 9 – 20 týdnů do přijímaček
MATEMATIKA
1. Navzájem opačné výrazy jsou takové výrazy, jejichž
(A) součin se rovná nule.
(B) součin se rovná jedné.
(C) rozdíl se rovná nule.
(D) součet se rovná jedné.
(E) součet se rovná nule.
Zvolíme si příklad: Opačné číslo k číslu 2 je -2.
Součin: 2 . (-2) = -4
Součet: 2 + (-2) = 0 --> E
Poznámka: Nezaměňovat s číslem převráceným: Převrácené číslo k číslu 2 je $\frac{1}{2}$
2. Na číselné ose jsou vyznačeny obrazy dvou čísel a, b:
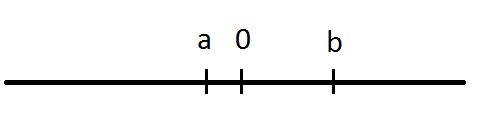
Ve které z následujících možností jsou všechna tři tvrzení pravdivá?
(A) a + b je záporné číslo, a – b je záporné číslo, a.b je kladné číslo.
(B) a + b je kladné číslo, a – b je kladné číslo, a.b je záporné číslo.
(C) a + b je kladné číslo, a – b je záporné číslo, a.b je záporné číslo.
(D) a + b je záporné číslo, a – b je záporné číslo, a.b je záporné číslo.
(E) a + b je záporné číslo, a – b je kladné číslo, a.b je kladné číslo.
Číslo a je vlevo od nuly, a proto je záporné. Číslo b je kladné a jeho absolutní hodnota je přibližně trojnásobná oproti číslu a. Zvolíme čísla a = -1, b = 3.
a + b = -1 + 3 = + 2 (kladné)
a - b = -1 - 3 = - 4 (záporné)
a . b = -1 . 3 = - 3 (záporné)
--> C
3. Kružnice k opsaná obdélníku KLMN na obrázku má střed v bodě S a poloměr 5 cm.
(A) $S=8 cm^2$
(B) $S=16 cm^2$
(C) $S=24 cm^2$
(D) $S=48 cm^2$
(E) $S=60 cm^2$
Strana a = 6 cm
Stranu b vypočteme pomocí Pythagorovy věty. Poloměr kružnice tvoří přeponu pravoúhlého trojúhelníku, tj. 5 cm, odvěsna má délku 3 cm. Trojúhelník, který má přeponu 5 cm a odvěsnu 3 cm, má druhou odvěsnu 4 cm.
Strana b = 2 . 4 cm = 8 cm
$S = a . b$
$S = 6 . 8$
$S = 48 cm^2$
--> D
4. 1 kg oříšků stojí 90 korun, 1 kg hrozinek stojí 50 korun a za půl kg mandlí zaplatíme 60 korun.
Kolik korun stojí 1 kg směsi, která vznikne smícháním 1 kg oříšků, 3 kg hrozinek a 1 kg mandlí?
(A) 132
(B) 120
(C) 90
(D) 72
(E) 40
1 kg oříšků = 1 . 90 Kč = 90 Kč
3 kg hrozinek = 3 . 50 Kč = 150 Kč
1 kg mandlí = 2 . 60 Kč = 120 Kč
4 kg směsi = 360 Kč
1 kg směsi = 90 Kč --> C
ČESKÝ JAZYK
Výchozí text 1 - 4
Vlaková souprava, jež měla osm vagónů, vjela do nádraží a dav lidí se vyhrnul na peron.
1. Určete slovní druhy:
vlaková - přídavné jméno
jež - zájmeno
nádraží - podstatné jméno
lidí - podstatné jméno
2. Proveďte grafický rozbor souvětí, určete druhy vedlejších vět a poměry mezi větami hlavními:
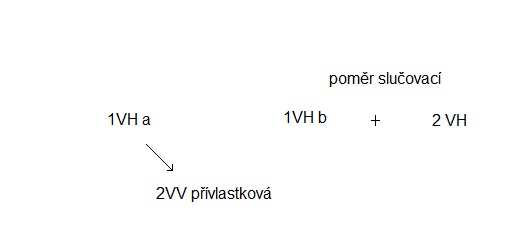
3. U všech sloves výchozího textu určete
|
|
osoba | číslo | čas | způsob | vid | rod | třída | vzor |
| měla | 3 | jednotné | minulý | oznamovací | nedokonavý | činný | 5 | dělá |
| vjela | 3 | jednotné | minulý | oznamovací | dokonavý | činný | 1 | umře |
| vyhrnul se | 3 | jednotné | minulý | oznamovací | dokonavý | činný | 2 | tiskne |
4. Z výchozího textu vypište neohebná slova a určete jejich slovní druhy.
do - předložka
a - spojka
na - předložka
5. Z výchozího textu vypište zájmena a číslovky a určete jejich druh.
osm - základní číslovka
jež - zájmeno vztažné
se - zájmeno osobní
6. Nahraďte slovo peron českým synonymem:
nástupiště
7. Vytvořte vidovou dvojici:
vjela - vjížděla